Tortendiagramme erstellen: Difference between revisions
(Übersetzung HOWTO Making a Pie Chart) |
C schaefer (talk | contribs) mNo edit summary |
||
| (3 intermediate revisions by one other user not shown) | |||
| Line 2: | Line 2: | ||
[[Category:DE]] | [[Category:DE]] | ||
Die Schwierigkeit ein Tortendiagramm in Scribus zu erzeugen besteht darin | Die Schwierigkeit, ein Tortendiagramm in Scribus zu erzeugen, besteht darin, daß – selbst wenn es einen Weg gäbe, mit den verschiedenen Zeichenwerkzeugen von Scribus eines zu erstellen – die Programmierung dafür viel zu aufwendig wäre. Wir benötigen also eine elegantere Lösung. Diese Lösung heißt SVG (Scalable Vector Graphics). | ||
Es funktioniert nicht einen Kreis zu zeichnen und anschließend zu teilen, denn wir wollen Segmente in verschiedenen Größen und jedes davon mit einer andern Füllfarbe. Auf dieser Seite zeige ich wie die notwendigen Informationen für das Python-Skript weiter unten zusammengestellt werden. | Es funktioniert nicht, einen Kreis zu zeichnen und anschließend zu teilen, denn wir wollen Segmente in verschiedenen Größen und jedes davon mit einer andern Füllfarbe. Auf dieser Seite zeige ich, wie die notwendigen Informationen für das Python-Skript weiter unten zusammengestellt werden. | ||
==SVG-Spezifikationen und Bögen zeichnen== | ==SVG-Spezifikationen und Bögen zeichnen== | ||
| Line 10: | Line 10: | ||
{| | {| | ||
|[[Image:Abcpie.png]] | |[[Image:Abcpie.png]] | ||
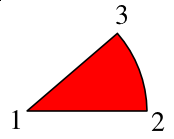
||Beginnen wir mit diesem Beispiel-Tortenstück (Kreissegment). Wir werden die SVG-Spezifikationen benutzen um dem Programm mitzuteilen wie diese Figur gezeichnet werden soll. Wir starten an Punkt 1, zeichnen eine Linie zu Punkt 2, dann einen Bogen von Punkt 2 nach Punkt 3 und zuletzt wieder eine Linie von Punkt 3 zu Punkt 1. | ||Beginnen wir mit diesem Beispiel-Tortenstück (Kreissegment). Wir werden die SVG-Spezifikationen benutzen, um dem Programm mitzuteilen, wie diese Figur gezeichnet werden soll. Wir starten an Punkt 1, zeichnen eine Linie zu Punkt 2, dann einen Bogen von Punkt 2 nach Punkt 3 und zuletzt wieder eine Linie von Punkt 3 zu Punkt 1. | ||
Hier ist der Pfad-Befehl dafür: | Hier ist der Pfad-Befehl dafür: | ||
| Line 18: | Line 18: | ||
</pre> | </pre> | ||
|} | |} | ||
Die erste Zeile legt die Richtungen fest. '''M''' ist der Befehl für den Ausgangspunkt | Die erste Zeile legt die Richtungen fest. '''M''' ist der Befehl für den Ausgangspunkt – der Kreis(Torten)mittelpunkt – und dieser liegt bei X=200 und Y=200 (links oben) in unserem SVG-Arbeitsraum. Alle folgenden Befehle in diesem Beispiel sind relativ zu diesem Ausgangspunkt. | ||
Mit dem Befehl '''I''' (X=150 und Y=0) wird eine Linie 150 Einheiten horizontal nach rechts gezogen, in der Vertikalen ändert sich nichts. ''(Für diese erste Linie hätte auch der '''h'''-Befehl | Mit dem Befehl '''I''' (X=150 und Y=0) wird eine Linie 150 Einheiten horizontal nach rechts gezogen, in der Vertikalen ändert sich nichts. ''(Für diese erste Linie hätte auch der '''h'''-Befehl – er zeichnet eine horizontale Linie – benutzt werden können, aber das Skript soll nicht nur für Segmente mit einer horizontalen Linie gelten)'' | ||
Nun zeichnen wir mit dem '''a''' Befehl den Bogen. Die Radien X und Y sind beide auf 150 gesetzt | Nun zeichnen wir mit dem '''a''' Befehl den Bogen. Die Radien X und Y sind beide auf 150 gesetzt – wären sie nicht gleich, dann hätten wir einen elliptischen Bogen. | ||
Als nächstes folgen drei Nullen von denen nur die mittlere für unser Tortendiagramm verändert werden muß: da wir nur zwei Punkte auf einem hypothetischen Kreis brauchen, | Als nächstes folgen drei Nullen, von denen nur die mittlere für unser Tortendiagramm verändert werden muß: da wir nur zwei Punkte auf einem hypothetischen Kreis brauchen, müssen wir festlegen, ob wir die kurze oder die lange Strecke um den Kreis herum gehen wollen. Die Null in der Mitte wählt den kurzen Weg (unser Tortenstück ist kleiner als die halbe Torte) | ||
Nun der komplizierte Teil: | Nun der komplizierte Teil: Die letzen zwei Zahlen (-39, -97) sind ''relative'' Abstände vom Punkt '''2''' zu Punkt '''3''' – kartesische X,Y-Koordinaten ''auf dem Monitor''. | ||
Das '''z''' zum Schluß gibt an daß die Figur geschlossen werden soll | Das '''z''' zum Schluß gibt an, daß die Figur geschlossen werden soll – zurück zu Punkt '''1'''. | ||
Und woher bekommen wir diese relativen Angaben zu unserem Bogen? | Und woher bekommen wir diese relativen Angaben zu unserem Bogen? '''Trigonometrie!''' | ||
==Verschüttete Trigonometriekenntisse reaktivieren== | ==Verschüttete Trigonometriekenntisse reaktivieren== | ||
Was repräsentieren Tortendiagramme? Tortendiagramme zeigen uns anschaulich die einzelnen Elemente einer Werteliste, wobei die Größe eines Tortenstückes vom jeweiligen Wert auf der Liste abhängt | Was repräsentieren Tortendiagramme? Tortendiagramme zeigen uns anschaulich die einzelnen Elemente einer Werteliste, wobei die Größe eines Tortenstückes vom jeweiligen Wert auf der Liste abhängt – die gesamte Torte entspricht der Summe dieser Werte. Um nun herauszufinden, wie groß das Tortenstück angezeigt werden soll, mußt Du den einzelnen Wert durch die Summe aller Werte auf der Liste teilen. Da die Torte 360° umfaßt, sieht die Formel so aus: | ||
<pre> | <pre> | ||
Winkel= [(Wert)/Summe aller Werte] × 360 | Winkel= [(Wert)/Summe aller Werte] × 360 | ||
</pre> | </pre> | ||
heraus kommt dabei der Winkel den das betreffende Tortenstück abdeckt. | heraus kommt dabei der Winkel, den das betreffende Tortenstück abdeckt. | ||
''Beispiel:'' | ''Beispiel:'' | ||
| Line 44: | Line 44: | ||
{| | {| | ||
|[[Image:123pie.png]] | |[[Image:123pie.png]] | ||
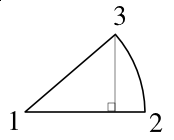
||Wir suchen nun die X,Y-Koordinaten von Punkt '''3''' in | ||Wir suchen nun die X,Y-Koordinaten von Punkt '''3''' in bezug auf den Anfangspunkt (den Kreismittelpunkt) – siehe die relativen Parameter, die weiter oben für die SVG-Figur benutzt wurden. Sobald wir diese Koordinaten wissen, subtrahieren wir sie von den Koordinaten des Punktes '''2''' – dann haben wir die relativen Werte für den SVG-Pfadbefehl. Stellen wir uns ein rechtwinkliges Dreieck mit der Linie '''1-3''' als Hypotenuse vor. Die Koordinaten von Punkt '''3''' sind X=Grundlinie (Ankathete) und Y=Höhe (Gegenkathete) des imaginären Dreieckes. Der Abstand '''1-3''' (Hypotenuse) ist unser Radius, also können wir über Winkelfunktionen den Winkel unseres Tortenstückes bestimmen: | ||
{| cellpadding="8px" | | {| cellpadding="8px" | | ||
| Line 57: | Line 57: | ||
|} | |} | ||
{| | {| | ||
|Wie geht es mit dem nächsten Segment weiter? Wir bleiben bei unserer Startlinie als X-Achse für unsere Berechnungen. Für die folgenden Segmente gilt weiterhin unser Anfangspunkt. Wir | |Wie geht es mit dem nächsten Segment weiter? Wir bleiben bei unserer Startlinie als X-Achse für unsere Berechnungen. Für die folgenden Segmente gilt weiterhin unser Anfangspunkt. Wir müssen nicht die Winkel für jedes Segment kennen, sondern benötigen nur die "Eck"-Punkte der Bögen für unsere SVG-Berechnung. | ||
Addiere den Wert des ersten Tortenstückes zum Wert des zweiten hinzu und teile diese Summe durch die gesamte Torte (360°) für die Unterteilung der Torte | Addiere den Wert des ersten Tortenstückes zum Wert des zweiten hinzu und teile diese Summe durch die gesamte Torte (360°) für die Unterteilung der Torte | ||
| Line 67: | Line 67: | ||
Wenn wir nun die Sinus- und Cosinusformel von weiter oben mit diesem stumpfen Winkel benutzen, erhalten wir als Ergebnis die X,Y-Koordinaten für den Punkt '''4'''. | Wenn wir nun die Sinus- und Cosinusformel von weiter oben mit diesem stumpfen Winkel benutzen, erhalten wir als Ergebnis die X,Y-Koordinaten für den Punkt '''4'''. | ||
Wir können uns rund um die Torte | Wir können uns rund um die Torte herumarbeiten und mit den relativen Berechnungen für alle Punkte die Koordinaten ermitteln wie in piechart.py. Vom mathematischen Standpunkt aus erhält man genauere Ergebnisse, wenn immer vom gleichen Startpunkt aus gerechnet wird. Bei aufeinanderfolgenden Berechnungen, bei denen der Ausgangspunkt jedesmal verschoben ist, addieren sich Fehler durch geringfügige Ungenauigkeiten – als Ergebnis könnte beim letzten Kreissegment eine Lücke oder eine Überlappung auftreten. | ||
==piechart.py benutzen== | ==piechart.py benutzen== | ||
Wenn Du piechart.py startest ('''Script > Scripte für Scribus''') öffnet sich ein Eingabefenster mit der Frage nach einem Namen für die zu speichernde SVG-Datei. An den Namen den Du eingibst wird automatisch '''.svg''' angehängt. | Wenn Du piechart.py startest ('''Script > Scripte für Scribus'''), öffnet sich ein Eingabefenster mit der Frage nach einem Namen für die zu speichernde SVG-Datei. An den Namen, den Du eingibst, wird automatisch '''.svg''' angehängt. | ||
Das nächste Eingabefenster erwartet die Daten | Das nächste Eingabefenster erwartet die Daten – die Werte, aus denen die Torte berechnet und erstellt wird. Sobald Du einen Wert eingegeben hast und OK klickst (oder die Eingabe-Taste drückst), erscheint dasselbe Eingabefenster (leer) wieder, so lange bis Du eine '''0''' eingibst oder Du die Eingabezeile leer läßt und OK Klickst bzw. die Eingabetaste drückst. | ||
Ein Meldungsfenster teilt Dir mit daß die Datei (im Skript-Ordner) erstellt wurde. | Ein Meldungsfenster teilt Dir mit, daß die Datei (im Skript-Ordner) erstellt wurde. | ||
Einen undokumentierten '''<tt>importSVG()</tt>''' Befehl habe ich auskommentiert, da dies | Einen undokumentierten '''<tt>importSVG()</tt>'''-Befehl habe ich auskommentiert, da dies in den Scribus-Versionen < 1.3.x nicht funktioniert. Auch wenn es in den 1.3.x -Versionen funktioniert, hat die neu eingefügte Seite eine andere Größe als das schon geöffnete Dokument – dieser Befehl ist also im Moment nicht sehr nützlich. Da es sich um einen undokumentierten Befehl handelt, ist nicht klar, ob andere Parameter dieses Verhalten korrigieren würden. | ||
{| cellpadding="10px" | | {| cellpadding="10px" | | ||
! !! Einige Beispiele !! | ! !! Einige Beispiele !! | ||
|- | |- | ||
| [[Image:Piechart1.png]] || Hier sind zwei Ausgabebeispiele aus gleichen Daten. Die rechte Torte | | [[Image:Piechart1.png]] || Hier sind zwei Ausgabebeispiele aus gleichen Daten. Die rechte Torte erhältst Du, wenn im Skript die Rahmenfarbe (bordercolor) auf '''none''' gesetzt wird, die Linienstärke (stroke-width) auf '''0''' oder Du den Form-Rahmen in Scribus ganz normal bearbeitest. || | ||
[[Image:Piechart2.png]] | [[Image:Piechart2.png]] | ||
|- | |- | ||
| [[Image:Piechart3.png]] || Dieses letzte Beispiel kann ganz einfach in Scribus | | [[Image:Piechart3.png]] || Dieses letzte Beispiel kann ganz einfach in Scribus bearbeitet werden: Zuerst löse die Gruppierung der SVG-Grafik auf ('''Kontextmenü''' (Rechtsklick auf das Objekt) ''' > Gruppierung auflösen''', Tastaturkürzel: '''Strg+U''')|| | ||
{| cellpadding="8px" | {| cellpadding="8px" | ||
|- | |- | ||
| | | | ||
|- | |- | ||
|valign="bottom" bgcolor="palegreen" | Nebenbei bemerkt, alle Abbildungen <br>auf dieser Wiki-Seite entstanden indem <br>Tortendiagramme mit piechart.py erstellt, in Scribus nachbearbeitet und als | |valign="bottom" bgcolor="palegreen" | Nebenbei bemerkt, alle Abbildungen <br>auf dieser Wiki-Seite entstanden, indem <br>Tortendiagramme mit piechart.py erstellt, in Scribus nachbearbeitet und als Screenshot gespeichert wurden. | ||
|} | |} | ||
|} | |} | ||
==Versuche das nicht zu Hause (in der Schule / | ==Versuche das nicht zu Hause (in der Schule / im Beruf)== | ||
{| | {| | ||
|Eine Bemerkung zum Zusammenhang von Ästhetik und genauer Darstellung: | |Eine Bemerkung zum Zusammenhang von Ästhetik und genauer Darstellung: | ||
Manchmal sieht man gekippte Tortensegmente, wahrscheinlich um es "besser aussehen" zu lassen. | Manchmal sieht man gekippte Tortensegmente, wahrscheinlich um es "besser aussehen" zu lassen. | ||
Dieses Beispiel zeigt was passiert wenn Du das tust. In beiden Abbildungen sind die Segmente jeweils aus den gleichen Daten erstellt. Obwohl die Segmente die gleiche Größe haben sollten sind sie klar erkennbar auf der rechten Seite ungleich | Dieses Beispiel zeigt, was passiert, wenn Du das tust. In beiden Abbildungen sind die Segmente jeweils aus den gleichen Daten erstellt. Obwohl die Segmente die gleiche Größe haben sollten, sind sie klar erkennbar auf der rechten Seite ungleich – die Position des Segments auf dem Kreis beeinflußt die Darstellungsgröße. | ||
|| [[Image:Piechart5.png]] | || [[Image:Piechart5.png]] | ||
|} | |} | ||
==piechartDE.py== | ==piechartDE.py== | ||
Das englische Original liegt hier: [[Making_a_Pie_Chart#piechart.py | piechart.py]] Im folgenden Skript sind die Fensterbezeichnungen, Meldungen und Kommentare übersetzt. | Das englische Original liegt hier: [[Making_a_Pie_Chart#piechart.py | piechart.py]] Im folgenden Skript sind die Fensterbezeichnungen, Meldungen und Kommentare ins Deutsche übersetzt. Speichere den Text als piechartDE.py ''(unter Windows in <code>C:\Programme\Scribus 1.3.x\share\scripts</code> – prüfe auch, ob dieser Pfad in den '''Allgemeinen Einstellungen > Allgemein''' als Pfad für die Skripte gesetzt ist)''. In diesem Ordner werden auch die erzeugten SVGs gespeichert. | ||
<pre> | <pre> | ||
| Line 187: | Line 187: | ||
</pre> | </pre> | ||
== | ==Zugabe== | ||
Was ist mit einer Legende für unser Tortendiagramm? Ganz einfach: | Was ist mit einer Legende für unser Tortendiagramm? Ganz einfach: | ||
* nach '''<tt>lasty = 0</tt>''' füge folgende Zeile ein: | * nach '''<tt>lasty = 0</tt>''' füge folgende Zeile ein: | ||
| Line 198: | Line 198: | ||
ykey = ykey + 35 | ykey = ykey + 35 | ||
</pre> | </pre> | ||
Wenn Du nun das abgeänderte Skript laufen läßt | Wenn Du nun das abgeänderte Skript laufen läßt, erhältst Du folgendes: | ||
{| cellpadding="30px" | {| cellpadding="30px" | ||
| align="right" |[[Image:Piechart4.png]] | | align="right" |[[Image:Piechart4.png]] | ||
| valign="top" width="40%" align="left"|In der Scribus-Dokumentation findest Du die Empfehlung Texte (z.B. die Werte, oder welche Art Daten dargestellt werden) zu diesem Kreisdiagramm in Scribus einzufügen | | valign="top" width="40%" align="left"|In der Scribus-Dokumentation findest Du die Empfehlung, Texte (z.B. die Werte, oder welche Art Daten dargestellt werden) zu diesem Kreisdiagramm in Scribus einzufügen – vor allem für den späteren PDF-Export ist das besser (Textauflösung) | ||
|} | |} | ||
Wenn Du keine Legende (oder einzelne Legendeneinträge) willst, kannst Du, wie weiter oben beschrieben, die Gruppierung der SVG-Grafik auflösen und entsprechend bearbeiten. Möglich wäre auch, ein weiteres Eingabefenster zu Beginn des Skriptes einzufügen und abzufragen, ob eine Legende gewünscht wird. Dazu wandle die '''<tt>L.append('<rect...</tt>''' Anweisung in eine '''<tt>if</tt>''' -Bedingung (abhängig von der Eingabe) um. Wenn Du keine Legende erstellen willst, spielen die Zuweisung und die Veränderungen in der '''<tt>ykey</tt>'''-Variablen keine Rolle. | |||
==Noch mehr?== | ==Noch mehr?== | ||
| Line 222: | Line 222: | ||
</pre> | </pre> | ||
Mit ein paar Veränderungen kannst Du einen Textrahmen zu piechart.py/piechartDE.py hinzufügen. | Mit ein paar Veränderungen kannst Du einen Textrahmen zu piechart.py/piechartDE.py hinzufügen. | ||
In diesem stehen dann die Zahlen die Du eingibst, sowie der prozentuale Wert den diese | In diesem stehen dann die Zahlen, die Du eingibst, sowie der prozentuale Wert, den diese Zahlen repräsentieren – für den Fall, daß Du das neben dem Tortendiagramm brauchst. Dieser Rahmen wird jedoch in Scribus erzeugt ''und nicht der SVG-Datei hinzugefügt''. | ||
Latest revision as of 01:43, 12 March 2007
| Installation • Anwendungsfragen • PDF-Export • DTP • Sonstiges |
Die Schwierigkeit, ein Tortendiagramm in Scribus zu erzeugen, besteht darin, daß – selbst wenn es einen Weg gäbe, mit den verschiedenen Zeichenwerkzeugen von Scribus eines zu erstellen – die Programmierung dafür viel zu aufwendig wäre. Wir benötigen also eine elegantere Lösung. Diese Lösung heißt SVG (Scalable Vector Graphics).
Es funktioniert nicht, einen Kreis zu zeichnen und anschließend zu teilen, denn wir wollen Segmente in verschiedenen Größen und jedes davon mit einer andern Füllfarbe. Auf dieser Seite zeige ich, wie die notwendigen Informationen für das Python-Skript weiter unten zusammengestellt werden.
SVG-Spezifikationen und Bögen zeichnen
Für ausführliche Informationen über die SVG-Spezifikationen siehe hier
Die erste Zeile legt die Richtungen fest. M ist der Befehl für den Ausgangspunkt – der Kreis(Torten)mittelpunkt – und dieser liegt bei X=200 und Y=200 (links oben) in unserem SVG-Arbeitsraum. Alle folgenden Befehle in diesem Beispiel sind relativ zu diesem Ausgangspunkt. Mit dem Befehl I (X=150 und Y=0) wird eine Linie 150 Einheiten horizontal nach rechts gezogen, in der Vertikalen ändert sich nichts. (Für diese erste Linie hätte auch der h-Befehl – er zeichnet eine horizontale Linie – benutzt werden können, aber das Skript soll nicht nur für Segmente mit einer horizontalen Linie gelten)
Nun zeichnen wir mit dem a Befehl den Bogen. Die Radien X und Y sind beide auf 150 gesetzt – wären sie nicht gleich, dann hätten wir einen elliptischen Bogen. Als nächstes folgen drei Nullen, von denen nur die mittlere für unser Tortendiagramm verändert werden muß: da wir nur zwei Punkte auf einem hypothetischen Kreis brauchen, müssen wir festlegen, ob wir die kurze oder die lange Strecke um den Kreis herum gehen wollen. Die Null in der Mitte wählt den kurzen Weg (unser Tortenstück ist kleiner als die halbe Torte)
Nun der komplizierte Teil: Die letzen zwei Zahlen (-39, -97) sind relative Abstände vom Punkt 2 zu Punkt 3 – kartesische X,Y-Koordinaten auf dem Monitor. Das z zum Schluß gibt an, daß die Figur geschlossen werden soll – zurück zu Punkt 1.
Und woher bekommen wir diese relativen Angaben zu unserem Bogen? Trigonometrie!
Verschüttete Trigonometriekenntisse reaktivieren
Was repräsentieren Tortendiagramme? Tortendiagramme zeigen uns anschaulich die einzelnen Elemente einer Werteliste, wobei die Größe eines Tortenstückes vom jeweiligen Wert auf der Liste abhängt – die gesamte Torte entspricht der Summe dieser Werte. Um nun herauszufinden, wie groß das Tortenstück angezeigt werden soll, mußt Du den einzelnen Wert durch die Summe aller Werte auf der Liste teilen. Da die Torte 360° umfaßt, sieht die Formel so aus:
Winkel= [(Wert)/Summe aller Werte] × 360
heraus kommt dabei der Winkel, den das betreffende Tortenstück abdeckt.
Beispiel: Wert=25, Summe aller Werte=100 (der Wert entspricht also einem Viertel -> ein Viertelkreis für das Segment (90°)
[(25/100)] * 360 = 90
| Wie geht es mit dem nächsten Segment weiter? Wir bleiben bei unserer Startlinie als X-Achse für unsere Berechnungen. Für die folgenden Segmente gilt weiterhin unser Anfangspunkt. Wir müssen nicht die Winkel für jedes Segment kennen, sondern benötigen nur die "Eck"-Punkte der Bögen für unsere SVG-Berechnung.
Addiere den Wert des ersten Tortenstückes zum Wert des zweiten hinzu und teile diese Summe durch die gesamte Torte (360°) für die Unterteilung der Torte Winkel = [(Wert1 + Wert2)/Summe aller Werte] × 360 |

|
Wenn wir nun die Sinus- und Cosinusformel von weiter oben mit diesem stumpfen Winkel benutzen, erhalten wir als Ergebnis die X,Y-Koordinaten für den Punkt 4.
Wir können uns rund um die Torte herumarbeiten und mit den relativen Berechnungen für alle Punkte die Koordinaten ermitteln wie in piechart.py. Vom mathematischen Standpunkt aus erhält man genauere Ergebnisse, wenn immer vom gleichen Startpunkt aus gerechnet wird. Bei aufeinanderfolgenden Berechnungen, bei denen der Ausgangspunkt jedesmal verschoben ist, addieren sich Fehler durch geringfügige Ungenauigkeiten – als Ergebnis könnte beim letzten Kreissegment eine Lücke oder eine Überlappung auftreten.
piechart.py benutzen
Wenn Du piechart.py startest (Script > Scripte für Scribus), öffnet sich ein Eingabefenster mit der Frage nach einem Namen für die zu speichernde SVG-Datei. An den Namen, den Du eingibst, wird automatisch .svg angehängt.
Das nächste Eingabefenster erwartet die Daten – die Werte, aus denen die Torte berechnet und erstellt wird. Sobald Du einen Wert eingegeben hast und OK klickst (oder die Eingabe-Taste drückst), erscheint dasselbe Eingabefenster (leer) wieder, so lange bis Du eine 0 eingibst oder Du die Eingabezeile leer läßt und OK Klickst bzw. die Eingabetaste drückst.
Ein Meldungsfenster teilt Dir mit, daß die Datei (im Skript-Ordner) erstellt wurde.
Einen undokumentierten importSVG()-Befehl habe ich auskommentiert, da dies in den Scribus-Versionen < 1.3.x nicht funktioniert. Auch wenn es in den 1.3.x -Versionen funktioniert, hat die neu eingefügte Seite eine andere Größe als das schon geöffnete Dokument – dieser Befehl ist also im Moment nicht sehr nützlich. Da es sich um einen undokumentierten Befehl handelt, ist nicht klar, ob andere Parameter dieses Verhalten korrigieren würden.
| Einige Beispiele | ||||
|---|---|---|---|---|
 |
Hier sind zwei Ausgabebeispiele aus gleichen Daten. Die rechte Torte erhältst Du, wenn im Skript die Rahmenfarbe (bordercolor) auf none gesetzt wird, die Linienstärke (stroke-width) auf 0 oder Du den Form-Rahmen in Scribus ganz normal bearbeitest. | |||
 |
Dieses letzte Beispiel kann ganz einfach in Scribus bearbeitet werden: Zuerst löse die Gruppierung der SVG-Grafik auf (Kontextmenü (Rechtsklick auf das Objekt) > Gruppierung auflösen, Tastaturkürzel: Strg+U) |
|
Versuche das nicht zu Hause (in der Schule / im Beruf)
| Eine Bemerkung zum Zusammenhang von Ästhetik und genauer Darstellung:
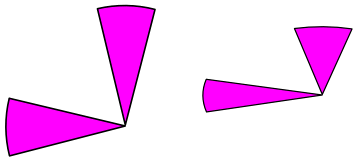
Manchmal sieht man gekippte Tortensegmente, wahrscheinlich um es "besser aussehen" zu lassen. Dieses Beispiel zeigt, was passiert, wenn Du das tust. In beiden Abbildungen sind die Segmente jeweils aus den gleichen Daten erstellt. Obwohl die Segmente die gleiche Größe haben sollten, sind sie klar erkennbar auf der rechten Seite ungleich – die Position des Segments auf dem Kreis beeinflußt die Darstellungsgröße. |
|
piechartDE.py
Das englische Original liegt hier: piechart.py Im folgenden Skript sind die Fensterbezeichnungen, Meldungen und Kommentare ins Deutsche übersetzt. Speichere den Text als piechartDE.py (unter Windows in C:\Programme\Scribus 1.3.x\share\scripts – prüfe auch, ob dieser Pfad in den Allgemeinen Einstellungen > Allgemein als Pfad für die Skripte gesetzt ist). In diesem Ordner werden auch die erzeugten SVGs gespeichert.
#!/usr/bin/env python
# File piechart.py
# Created 2006-05-29
# Gregory Pittman
# Übersetzung der Captions, Meldungen, Kommentare
# 04. Februar 2007 Uchiki
# Erstellt automatisch ein Tortendiagramm als SVG-Datei
# aus einer Werteliste
# Skript funktioniert unter Scribus Versionen 1.2.4.1 und 1.3.x
##########################################
from __future__ import division
import math
import scribus
# Wir erstellen eine Liste L, geben Werte ein, und kopieren die Liste zum Ende in eine Datei
L = ['<?xml version="1.0" encoding="UTF-8" standalone="no"?>\n']
L.append('<!DOCTYPE svg PUBLIC "-//W3C//DTD SVG 1.1//EN"\n')
L.append('"http://www.w3.org/Graphics/SVG/1.1/DTD/svg11.dtd">\n')
L.append('<svg width="20cm" height="20cm" xmlns="http://www.w3.org/2000/svg" version="1.1">\n')
svgfile = scribus.valueDialog('SVG Datei','Name der SVG-Datei\n".svg" wird automatisch angehängt')
svgfile = svgfile + '.svg'
sectors = []
while 1:
newvalue = scribus.valueDialog('Dateneingabe','Werte für die einzelnen Segmente des Tortendiagrammes eingeben\n- zum
Beenden 0 eingeben oder leere Eingabezeile')
if (newvalue == ''):
newvalue = '0'
newnum = float(newvalue)
if newnum == 0:break
sectors.append(newnum)
total = 0
i = 0
seg = 0
radius = 150
startx = 200 # X-Koordinate (Monitor) des Anfangspunktes : Mittelpunkt der Torte
starty = 200 # Y-Koordinate (Monitor) des Anfangspunktes : Mittelpunkt der Torte
lastx = radius # Start Koordinaten des
lasty = 0 # ersten Bogens
# Falls Dir die Farben nicht gefallen -- hier kannst Du andere angeben
# Wenn Du mehr als 9 Farben brauchst, kannst Du die Liste um so viele wie Du willst erweitern
colors = ['red','blue','yellow','magenta','orange','slateblue','slategrey','greenyellow','wheat']
bordercolor = 'black'
for n in sectors:
total = total + n # im voraus zu berechnen, da wir die Summe für die folgende Schleife
# brauchen
for n in sectors:
arc = "0" # zeichnet kurzen Bogen (< 180 Grad)
seg = n/total * 360 + seg # aktueller Winkel plus alle vorausgegangenen
if ((n/total * 360) > 180): # für den Fall das dieses Segment > 180 Grad ist
arc = "1"
radseg = math.radians(seg) # Konvertierung zu radians für Cosinus-, Sinusfunktion
nextx = int(math.cos(radseg) * radius)
nexty = int(math.sin(radseg) * radius)
# Das Minuszeichen steht hier (-(lasty)), da in unserer Berechnung der Y-Wert des Graphen die
# positiven Zahlen 'nach oben' bedeuten, auf dem Monitor jedoch bedeuten sie 'nach unten'.
L.append('<path d="M '+str(startx)+','+str(starty) + ' l '+str(lastx)+','+str(-(lasty))+' a' + str(radius) + ',' +
str(radius) + ' 0 ' + arc + ',0 '+str(nextx - lastx)+','+str(-(nexty - lasty))+ ' z" \n')
L.append('fill="'+colors[i]+'" stroke="' + bordercolor + '" stroke-width="2" stroke-linejoin="round" />\n')
# Wir schreiben die XML-Befehle für jedes Segment einzeln und vergessen die alten Punkte die
# nicht mehr gebraucht werden; nextx wird zu lastx für das darauffolgende Segment
lastx = nextx
lasty = nexty
i += 1
L.append('</svg>') # End-Tag für die SVG-Datei
output = open(svgfile,'w') # Wir haben alles berechnet und die Liste L
output.writelines(L) # mit unseren Befehlen erstellt, jetzt wird
output.close() # alles in eine Datei geschrieben.
endmessage = svgfile + ' wurde erstellt\nund im Script-Ordner gespeichert'
scribus.messageBox("Fertig",endmessage,icon=0,button1=1) # Meldungsfenster zur Information
# if scribus.haveDoc(): # Die letzte Anweisung ist auskommentiert - sie erstellt
# scribus.importSVG(svgfile) # eine neue Seite. Dies funktioniert aber nicht
# bei Scribus-Versionen vor <1.3.x
# Die SVG-Datei wird trotzdem gespeichert und kann
# manuell importiert werden.
Zugabe
Was ist mit einer Legende für unser Tortendiagramm? Ganz einfach:
- nach lasty = 0 füge folgende Zeile ein:
ykey = 25
- vor der Zeile lastx = nextx füge diese zwei Zeilen ein:
L.append('<rect x="375" y="'+ str(ykey) + '" width="40" height="30" fill="'+colors[i] + '" stroke="black" stroke-width="1"/>\n')
ykey = ykey + 35
Wenn Du nun das abgeänderte Skript laufen läßt, erhältst Du folgendes:

|
In der Scribus-Dokumentation findest Du die Empfehlung, Texte (z.B. die Werte, oder welche Art Daten dargestellt werden) zu diesem Kreisdiagramm in Scribus einzufügen – vor allem für den späteren PDF-Export ist das besser (Textauflösung) |
Wenn Du keine Legende (oder einzelne Legendeneinträge) willst, kannst Du, wie weiter oben beschrieben, die Gruppierung der SVG-Grafik auflösen und entsprechend bearbeiten. Möglich wäre auch, ein weiteres Eingabefenster zu Beginn des Skriptes einzufügen und abzufragen, ob eine Legende gewünscht wird. Dazu wandle die L.append('<rect... Anweisung in eine if -Bedingung (abhängig von der Eingabe) um. Wenn Du keine Legende erstellen willst, spielen die Zuweisung und die Veränderungen in der ykey-Variablen keine Rolle.
Noch mehr?
Sicher, aber das ist Deine "Hausaufgabe"
Schau Dir diesen Skriptausschnitt aus Creating a Graph, Part 2 an:
caption = "Scale for this graph\n\n" "X: " + str(xmark) + "units/mark\n" + "Y: "
caption = caption + str(ymark) + "units/mark\n" + str(xscale) + " pts/unit (X)\n"
caption = caption + str(yscale) + " pts/unit (Y)"
# These caption statements can be combined to one line
S = scribus.createText(200, 120, 150, 80)
scribus.setTextColor("Blue", S)
scribus.setText(caption, S)
scribus.setTextAlignment(1, S)
scribus.setFont("Nimbus Roman No9 L Bold", S)
scribus.setFontSize(8, S)
Mit ein paar Veränderungen kannst Du einen Textrahmen zu piechart.py/piechartDE.py hinzufügen. In diesem stehen dann die Zahlen, die Du eingibst, sowie der prozentuale Wert, den diese Zahlen repräsentieren – für den Fall, daß Du das neben dem Tortendiagramm brauchst. Dieser Rahmen wird jedoch in Scribus erzeugt und nicht der SVG-Datei hinzugefügt.