Making a Pie Chart

The difficulty with making a pie chart with Scribus is that, if there is a way to use the various drawing tools to do it, the programming is quite beyond anything one would want to tackle. What we need then, is a more elegant way. Fortunately, with SVGs, there is a way.

What you cannot do is draw a circle, then subdivide it, because what we really want is a series of segments like variably sized pieces of pie, each of which can have its own fill color. What I want to show in this page is the process of putting information together to make the python script you will find at the end.

SVG Specifications and Drawing Arcs

For the details and much more information about SVG specifications, check this link.

Let's start with this idealized pie chart segment. It turns out that the way we are going to use SVG specs to tell a program how to draw this shape is to start with point 1, draw a line to point 2, then draw the arc from 2 to 3, then go back to 1. Here is the path command that will accomplish this: <path d="M 200,200 l 150,0 a150,150 0 0,0 -37,-97 z" fill="red" stroke="black" stroke-width="2" stroke-linejoin="round" />

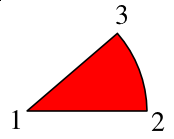
The first line shows our directions. M is the command for our starting point, the center of our pie circle, and relates to a point relative to the screen origin of our SVG space -- the upper left hand corner. After this all subsequent commands will be relative ones (in this example). Next the l says to draw a line from the starting point 150 X-units, but Y stays the same. (For this first segment, we could have used the h command, which will draw a horizontal line, but we need to generalize our process, and most or all of the other segments will not have a horizontal line.)

Now we draw our arc, using the a command, which is followed by X and Y radii, each of which we have set to 150 -- if they were not equal, we would be drawing an elliptical arc. Next are three zeros, but only the middle might be changed. Since we are only specifying two points along a hypothetical circle, we need to specify whether we will take the short route or the long route around the circle. Our middle zero says to take the short route (our piece of pie is less than half the pie).

Now, the tricky part. The last two numbers (-37, -97) are the relative distances from point 2 to point 3, in Cartesian X,Y computer-display coordinates. Finally, the z at the end says to complete this shape to a closed form -- go back to point 1.

How do we figure out these relative measurements along our arc? Trigonometry.