Making a Pie Chart: Difference between revisions
| Line 124: | Line 124: | ||
for n in sectors: | for n in sectors: | ||
arc = "0" | arc = "0" # default is to draw short arc (< 180 degrees) | ||
seg = n/total * 360 + seg # this angle will be current plus all previous | seg = n/total * 360 + seg # this angle will be current plus all previous | ||
if ((n/total * 360) > 180): # just in case this piece is > 180 degrees | if ((n/total * 360) > 180): # just in case this piece is > 180 degrees | ||
| Line 154: | Line 154: | ||
# but file will still be saved and can be manually imported | # but file will still be saved and can be manually imported | ||
</pre> | </pre> | ||
==But wait! There's more!== | ==But wait! There's more!== | ||
What about a key for our piechart? Easy. | What about a key for our piechart? Easy. | ||
Revision as of 03:39, 3 June 2006
The difficulty with making a pie chart with Scribus is that, if there is a way to use the various drawing tools to do it, the programming is quite beyond anything one would want to tackle. What we need then, is a more elegant way. Fortunately, with SVGs, there is a way.
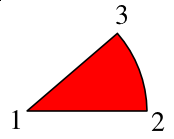
What you cannot do is draw a circle, then subdivide it, because what we really want is a series of segments like variably sized pieces of pie, each of which can have its own fill color. What I want to show in this page is the process of putting information together to make the python script you will find at the end.
SVG Specifications and Drawing Arcs
For the details and much more information about SVG specifications, check this link.
The first line shows our directions. M is the command for our starting point, the center of our pie circle, and relates to a point relative to the screen origin of our SVG space -- the upper left hand corner. After this all subsequent commands will be relative ones (in this example). Next the l says to draw a line from the starting point 150 X-units, but Y stays the same. (For this first segment, we could have used the h command, which will draw a horizontal line, but we need to generalize our process, and most or all of the other segments will not have a horizontal line.)
Now we draw our arc, using the a command, which is followed by X and Y radii, each of which we have set to 150 -- if they were not equal, we would be drawing an elliptical arc. Next are three zeros, but only the middle might need to be changed for our pie chart. Since we are only specifying two points along a hypothetical circle, we need to specify whether we will take the short route or the long route around the circle. Our middle zero says to take the short route (our piece of pie is less than half the pie).
Now, the tricky part. The last two numbers (-37, -97) are the relative distances from point 2 to point 3, in Cartesian X,Y computer-display coordinates. Finally, the z at the end says to complete this shape to a closed form -- go back to point 1.
How do we figure out these relative measurements along our arc? Trigonometry.
Trigonometry Awakens
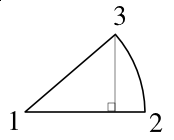
Let's think about what pie charts represent. Pie charts merely show us visually how some whole list of data values is subdivided into its components, with the size of each piece corresponding to the size of its share of the pie. So to know how big this piece should display, I need to divide it by the total size of the pie. Since the circle of our pie spans 360°, our formula looks like this:
angle = [(size of piece)/total] × 360
which gives us the angle of the circle occupied by our segment.
| But what about the next segment? We relied on the starting line being along the X-axis for our calculations. For the subsequent segments, let's stay with that reference point. We don't necessarily need to know the angle occupied by each segment, what we need are the corner points for our SVG calculations.
Add the original data value for the first pie piece to the value of the second, and divide that by the total, for the fraction of our pie circle: angle = [(size of piece A + size of piece B)/total] × 360 |

|
Now if we use our cosine and sine formulas again with this obtuse angle, we will get the correct X,Y values for point 4.
Eventually, we work our way around the pie, so that we have the coordinates for all these points, and once we have that, we make the relative calculations you see in piechart.py. From a mathematical point-of-view, we end up with more consistent results when we calculate from the same starting point. If we made successive calculations by shifting the reference point, we are likely to see additive errors related to the slight imprecision of our calculations -- the result might be either a gap or an overlap with the final segment.
Using piechart.py
When you start piechart.py, you first get a requestor asking for the filename to save to. Whatever you enter, ".svg" will be appended to your name.
Next a requestor appears asking for data -- your data values from which the calculations and pie chart will be created. After you enter one number, the requestor appears again and will keep reappearing until you press Enter with no entry, or enter "0" (the number).
A message box appears telling you that the file has been created.
While there is an undocumented importSVG() command in Scripter, I have commented this out in the script below. The reason is that, first of all, it does not work in Scribus versions < 1.3.x, and secondly, even when it works, it creates a new page, whose dimensions are different from the current document, so it does not seem especially useful at this time. Since it's an undocumented command, there may be other parameters which might fix this behavior.
| Some Examples | ||||
|---|---|---|---|---|
 |
Here are two examples of output with the same data. The one on the right can be made by changing piechart.py so that the bordercolor is 'none', setting the stroke-width to "0", or editing in Scribus. | |||
 |
This last example can easily be done in Scribus -- first ungroup the SVG (Item > Ungroup, keyboard: Ctrl+Shift+G, or find in Context Menu - right-click on SVG). Then individual segments can be selected and manipulated/edited in various ways. If you want to change the fill color of an individual segment, you must ungroup first. |
|
piechart.py
#!/usr/bin/env python
# File piechart.py
# Created 2006-05-29
# Gregory Pittman
# Automatically creates a piechart SVG file
# from a list of data
##########################################
from __future__ import division
import math
import scribus
# We'll create a list L, append to it, then copy the list to a file at the end
L = ['<?xml version="1.0" encoding="UTF-8" standalone="no"?>\n']
L.append('<!DOCTYPE svg PUBLIC "-//W3C//DTD SVG 1.1//EN"\n')
L.append('"http://www.w3.org/Graphics/SVG/1.1/DTD/svg11.dtd">\n')
L.append('<svg width="20cm" height="20cm" xmlns="http://www.w3.org/2000/svg" version="1.1">\n')
svgfile = scribus.valueDialog('SVG File','Enter name of file to save to\n".svg" will be appended')
svgfile = svgfile + '.svg'
sectors = []
while 1:
newvalue = scribus.valueDialog('Data Entry','Enter Data\n Enter 0 or no value to End')
if (newvalue == ''):
newvalue = '0'
newnum = float(newvalue)
if newnum == 0:break
sectors.append(newnum)
total = 0
i = 0
seg = 0
radius = 150
startx = 200 # The screen x-origin: center of pie chart
starty = 200 # The screen y-origin: center of pie chart
lastx = radius # Starting coordinates of
lasty = 0 # the first arc
colors = ['red','blue','yellow','magenta','orange','slateblue','slategrey','greenyellow','wheat']
bordercolor = 'black'
for n in sectors:
total = total + n # we have to do this ahead, since we need the total for the next for loop
for n in sectors:
arc = "0" # default is to draw short arc (< 180 degrees)
seg = n/total * 360 + seg # this angle will be current plus all previous
if ((n/total * 360) > 180): # just in case this piece is > 180 degrees
arc = "1"
radseg = math.radians(seg) # we need to convert to radians for cosine, sine functions
nextx = int(math.cos(radseg) * radius)
nexty = int(math.sin(radseg) * radius)
# The weirdly placed minus signs [eg, (-(lasty))] are due to the fact that
# our calculations are for a graph with positive Y values are up, but on the
# screen positive Y values go down.
L.append('<path d="M '+str(startx)+','+str(starty) + ' l '+str(lastx)+','+str(-(lasty))+' a' + radius + ',' + radius + ' 0 ' + arc + ',0 '+str(nextx - lastx)+','+str(-(nexty - lasty))+ ' z" \n')
L.append('fill="'+colors[i]+'" stroke="' + bordercolor + '" stroke-width="2" stroke-linejoin="round" />\n')
# We are writing the XML commands one segment at a time, so we abandon old points
# we don't need anymore, and nextx becomes lastx for the next segment
lastx = nextx
lasty = nexty
i += 1
L.append('</svg>')
output = open(svgfile,'w') # We've done all the calculations and filled
output.writelines(L) # up list L with our commands, so now we just
output.close() # write to a file all at once.
endmessage = svgfile + ' was created'
scribus.messageBox("Finished",endmessage,icon=0,button1=1) # Just for some user feedback
# if scribus.haveDoc(): # Commented out because it creates a new page
# scribus.importSVG(svgfile) # If you are using <1.3.x versions of Scribus, this would fail
# but file will still be saved and can be manually imported
But wait! There's more!
What about a key for our piechart? Easy. Somewhere around the line lasty = 0 add this line:
ykey = 25
Then just before the line lastx = nextx add these two lines:
L.append('<rect x="375" y="'+ str(ykey) + '" width="40" height="30" fill="'+colors[i] + '" stroke="black" stroke-width="1"/>\n')
ykey = ykey + 35
So now, when we run this new modified script, we get:

|
A recommendation you will find in the Scribus Documentation is that when you get ready to add text labels and any other annotations to this piechart, you will want to do these in Scribus, since this will lead to a better result in your eventual PDF as far as text resolution. |
Could there POSSIBLY be more?
Sure, but consider that your homework.
Look at this fragment from Creating a Graph, Part 2:
caption = "Scale for this graph\n\n" "X: " + str(xmark) + "units/mark\n" + "Y: "
caption = caption + str(ymark) + "units/mark\n" + str(xscale) + " pts/unit (X)\n"
caption = caption + str(yscale) + " pts/unit (Y)"
# These caption statements can be combined to one line
S = scribus.createText(200, 120, 150, 80)
scribus.setTextColor("Blue", S)
scribus.setText(caption, S)
scribus.setTextAlignment(1, S)
scribus.setFont("Nimbus Roman No9 L Bold", S)
scribus.setFontSize(8, S)
With some modifications you could add a text frame to piechart.py, giving you the numbers you added and the percentages of the total they represent, just in case you need that for your annotations. Just remember, you will print the text frame on your page, not add it to the SVG.